Коэффициент корреляции Пирсона
Коэффициент корреляции Пирсона r, который является безразмерным индексом в интервале от -1,0 до 1,0 включительно, отражает степень линейной зависимости между двумя множествами данных.
Показатель тесноты связи между двумя признаками определяется по формуле линейного коэффициента корреляции:
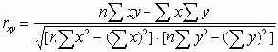
где x - значение факторного признака;
y - значение результативного признака;
n - число пар данных.
Парная корреляция - это связь между двумя признаками: результативным и факторным или двумя факторными.
Варианты связи, характеризующие наличие или отсутствие линейной связи между признаками:
• большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция) -наличие прямой линейной связи;
• малые значения одного набора связаны с большими значениями другого (отрицательная корреляция) -наличие отрицательной линейной связи;
• данные двух диапазонов никак не связаны (нулевая корреляция) -отсутствие линейной связи.
В качестве примера возьмем набор данных А (таблица 8.1). Необходимо определить наличие линейной связи между признаками x и y.
Для графического представления связи двух переменных использована система координат с осями, соответствующими переменным x и y. Построенный график, называемый диаграммой рассеивания, показан на рис. 8.2. Данная диаграмма показывает, что низкие значения переменной x соответствуют низким значениям переменной y, высокие значения переменной x соответствуют высоким значениям переменной y. Этот пример демонстрирует наличие явной связи.
